2.1 Tangent Graphs

Tangent Graphs

Plot of the Tangent Function

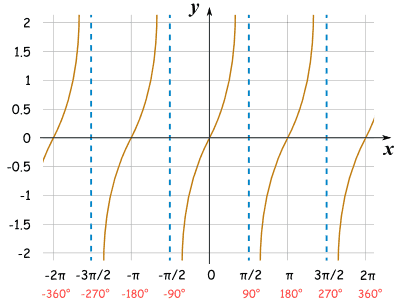
The Tangent function has a completely different shape ... it goes between negative and positive Infinity, crossing through 0 (every π radians, or 180°), as shown on this plot.

At π/2 radians, or 90° (and -π/2, 3π/2, etc) the function is officially undefined, because it could be positive Infinity or negative Infinity.

COTANGENT

Cotangent also known as cot,is a graph of 1/tangent. 

The cotangent function has asymptotes at $0$0, $\pi$π and at every positive and negative integer multiple of $\pi$π. It is periodic with period $\pi$π. It takes the value $0$0 at $\frac{\pi}{2}\pm n\pi$π2​±nπ for every integer $n$n. It is a decreasing function, meaning the graph always slopes downwards to the right.

The cotangent function is the reciprocal of the tangent function. That is, $\cot x=\frac{1}{\tan x}$cotx=1tanx​.

It is also true that $\cot x=\tan\left(\frac{\pi}{2}-x\right)=-\tan\left(x-\frac{\pi}{2}\right)$cotx=tan(π2​−x)=−tan(x−π2​). The form on the right of this identity makes it clear that the graph of the cotangent function is obtained by translating the graph of the tangent function to the right by $\frac{\pi}{2}$π2​ and then reflecting the result in the horizontal axis.