2.2 Sine Graphs

Sine Graphs

Plot of Sine

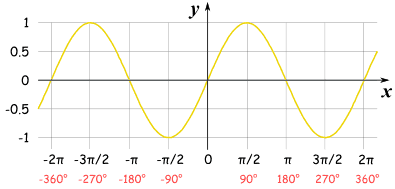
The Sine Function has this beautiful up-down curve (which repeats every 2π radians, or 360°).

It starts at 0, heads up to 1 by π/2 radians (90°) and then heads down to -1.



COSECANT


Cosecant also known as cosec, is a graph of 1/sine.

The cosecant function has asymptotes at $0\pm n\pi$0±nπ. It has local minima at $\frac{\pi}{2}\pm2n\pi$π2​±2nπ and local maxima at $\frac{3\pi}{2}\pm2n\pi$3π2​±2nπ. 

Since $\sin(-x)=-\sin x$sin(−x)=−sinx it follows that $\csc(-x)=-\csc x$csc(−x)=−cscx and so, $\csc x$cscx is an odd function. Its symmetry is captured by the statement $\csc x=-\csc(-x)$cscx=−csc(−x) which says that the graph of $\csc x$cscx looks the same after reflection in the vertical axis and then, reflection in the horizontal axis.

Starting from the graph of $\sec x$secx, we can obtain the graph of $\csc x$cscx by a transformation. Since $\csc x=\sec\left(\frac{\pi}{2}-x\right)$cscx=sec(π2​−x), we have $\csc x=\sec\left(x-\frac{\pi}{2}\right)$cscx=sec(x−π2​) (because $\sec$sec is an even function).

This says that we can obtain the graph of $\csc$csc by shifting the graph of $\sec$sec to the right by $\frac{\pi}{2}$π2​.